The L1 trend filtering - introduction.

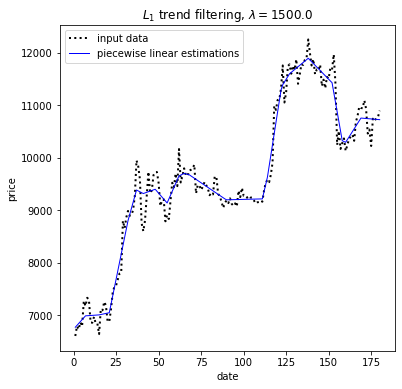
The problem of estimating underlying trends in time series data arises in a variety of disciplines. The ℓ1 trend filtering method produces trend estimates x that are piecewise linear from the time series y.

The ℓ1 trend estimation problem can be formulated as

$$ minimize \; (1/2) ||y-x||^2_2+λ||Dx||_1, $$

with variable $x$, problem data $y$ and parameter $λ$, with $λ\geq0$

where $D$ is the second difference matrix with rows

Editable input parameters in the example: problem data $y$ and parameter $λ.$

Example: L1 trend filtering for Bitcoin daily close.

The code and explanation are adopted from:

https://www.cvxpy.org/examples/applications/l1_trend_filter.html